Scope
Dynamical phenomena in network science include topics such as percolation, diffusion, and spreading models, random walks, and the onset of synchronization. General aim in understanding these phenomena is to unravel the relationship between the dynamics and the network structure. Prime real-world example in this setting would be understanding how large scale cortical networks of neurons collectively give rise to complicated observable phenomena such as conscious behavior. From the structural aspect it is important to have tools such as community detection and modularity/clustering analysis; in a wider scope one needs to be able to perform inference and learning on network and dynamical data. Recent years have also witnessed a surge of higher-order tools in network science such as topological data analysis.
The aim of this workshop is to bring together experts from the above topics to discuss current advances and to open new collaborations for tackling ambitious network problems.
This workshop will take place in the first week 29th April - 3rd May 2024 of the WINQ program.
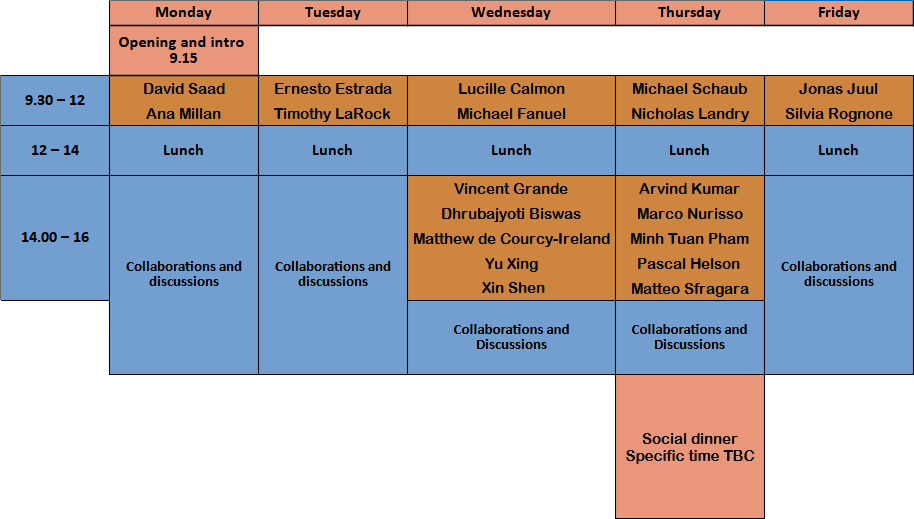
Schedule
Invited Speakers
Ernesto Estrada, Similarity and centrality of vertices in graphs/networks
Abstract: I consider the problem of detecting the group of vertices more similar to a given one in a graph/network. Starting from measures defined in the literature I analyze their main drawbacks. Then, I propose a metric based on the communicability cosine angle between pairs of vertices in a network. I then define a similarity measure based on it and illustrate that it solves the problems existing with previous measures. I then define a measure based on this similarity measure, which quantifies the communicability closeness centrality (CCC) of a vertex to the rest in a network. Using it I approach the problem of distinguishing all pairs of vertices which are not automorphically equivalent in a network. Finally, I illustrate the use of the CCC in ranking vertices in real-world networks, and illustrate its main differences with existing centrality measures like the degree, closeness, betweenness and eigenvector centrality.
Lucille Calmon, Networks for applied infectious disease epidemiology
Abstract: Contacts between individuals mediate the spread of infectious diseases in a population. Networks that describe these contacts thus crucially inform mathematical models of infectious diseases. In this talk, I will describe how such networks can be constructed, and discuss their implications for applied infectious disease epidemiology.
Michael Schaub, Learning the effective order of a hypergraph dynamical system
Abstract: Dynamical systems on hypergraphs can display a rich set of behaviours not observable for systems with pairwise interactions. Given a distributed dynamical system with a putative hypergraph structure, an interesting question is thus how much of this hypergraph structure is actually necessary to faithfully replicate the observed dynamical behaviour. To answer this question, we propose a method to determine the minimum order of a hypergraph necessary to approximate the corresponding dynamics accurately. Specifically, we develop an analytical framework that allows us to determine this order when the type of dynamics is known. We utilize these ideas in conjunction with a hypergraph neural network to directly learn the dynamics itself and the resulting order of the hypergraph from both synthetic and real data sets consisting of observed system trajectories.
Ana P. Millán, Explosive synchronization of higher-order Kuramoto oscillators
Abstract: From social interactions to the human brain, networks, and their higher-order counterpart are key to describing the underlying structure and dynamics of complex systems. While it is well known that network structure strongly affects its function, the role that the underlying geometry and topology play on the emergent dynamical properties of a system is yet to be clarified. Yet recent experimental studies are pointing out the fundamental role of these higher-order effects in understanding the behavior of complex systems. As an example, I will discuss the presence of higher-order coupling in functional brain networks, and their association with neurophysiological disorders [2].
I will consider the role of the higher-order organization in synchronization dynamics, and in particular in the Kuramoto model, going from node synchronization on networks with an underlying higher-order structure, to the synchronization of higher-order topological signals, associated not only with the nodes of a system but in general with any of its higher-dimensional components or simplices: links, triangles, tetrahedra, and so on. Whereas nodes interact only through links, higher-order simplices in general may interact both through their lower- and higher-dimensional faces. I will present the higher-order Kuramoto model, which defines the synchronization dynamics of n-dimensional simplices based on the n-dimensional Hodge Laplacian. I will show how, depending on whether there exists coupling between the upper- and lower-dimensional faces of the simplices, the emergent synchronization transition is of a continuous or discontinuous nature. Remarkably, in either case, the topological transition cannot be observed via the standard Kuramoto order parameter, but it requires the application of topological filters to retain only the solenoidal or irrotational components of the data.
[1] Ana P. Millán, Joaquín J. Torres and Ginestra Bianconi. Explosive higher-order Kuramoto dynamics on simplicial complexes. Physical Review L 124.21, 218301 (2021).
[2] Fernando A.N. Santos, P. K.B. Tewarie, P. Baudot, A. Luchicchi, D. Barros de Souza, G. Girier, A.P. Milan et al. Emergence of high-order functional hubs in the human brain. bioRxiv (2023): 2023-02. doi: https://doi.org/10. 1101/2023.02.10.528083
[3] Ana P. Millán, Juan G. Restrepo, Joaquín J. Torres and Ginestra Bianconi. Geometry, topology and simplicial synchronization in Higher-Order Systems. (pp. 268-299) (Springer International Publishing, 2022).
David Saad, Optimisation and mitigation of spreading processes
Abstract: The modern world comprises interlinked networks of contacts between individuals, computing devices and social groups, where infectious diseases, information and opinions propagate through their edges in a probabilistic or deterministic manner via interactions between individual constituents. The spread of information, opinions and marketing material can be modelled and analysed in a similar manner to that of epidemic spreading among humans or animals.
To contain and mitigate the spread of infectious diseases one would like to model the spread accurately, implement effective prevention and mitigation policies and deploy vaccines in a way that minimises the spread. This is a difficult problem and becomes even harder in the presence of infectious but asymptomatic individual states. In the world of marketing and opinion setting, winners are those who maximise the impact by deploying resource to the most influential available nodes at the right time, occasionally in competition (or collaboration) with adversarial (supportive) spreading processes. These can represent opinion formation by political parties (competitive) or diseases that increase the susceptibility to mutual infections (collaborative). Additionally, spreading processes on different networks may be interlinked, providing additional challenge in their mitigation.
I will explain the modelling of epidemic spreading processes and present the probabilistic analytical framework for impact maximisation/minimisation we have developed, addressing the questions of vaccine (budget) deployment and spreading maximisation in single and competitive/collaborative processes. I will also present the analysis of epidemic spreading processes with infectious but asymptomatic states and of interlinked spreading processes on different networks, and the effectiveness of containment and mitigation in both cases.
A. Y. Lokhov and D. Saad, Proc. of the National Academy of Sci., 114 E8138 (2017).
H. Sun, D. Saad and A. Y. Lokhov, Phys. Rev. X, 11, 011048 (2021).
B. Li and D. Saad, Phys. Rev. E 103, 052303 (2021).
B. Li and D. Saad, arxiv.org/html/2307.16767v3 (2023).
Silvia Rognone, A dynamical perspective on the geometrical characterization of cities
Timothy LaRock, Encapsulation Structure and Dynamics in Hypergraphs
Abstract: Hypergraphs are a powerful modelling framework to represent systems where interactions may involve an arbitrary number of nodes. In this talk we will explore the extent to which smaller hyperedges are subsets of larger hyperedges in real-world and synthetic hypergraphs, a property that we call encapsulation. Building on the concept of line graphs, we develop measures to quantify the relations existing between hyperedges of different sizes and, as a byproduct, the compatibility of the data with a simplicial complex representation, whose encapsulation would be maximum. We then turn to the impact of the observed structural patterns on diffusive dynamics, focusing on a variant of threshold models, called encapsulation dynamics, and demonstrate that non-random patterns can accelerate the spreading in the system.
Michaël Fanuel, Sparsification of the magnetic Laplacian and a cyclepopping random walk
Abstract: Graph Laplacians have applications in several areas of applied mathematics such as network science, machine learning, control, etc. In this talk, we consider the problem of finding a controlled approximation of a Laplacian matrix - called a sparsifier - which only has a few non-zero entries. This (sparse) matrix is associated with a graph with fewer edges, and is often cheaper to inverse. Sparsifiers are particularly useful for building preconditioners of Laplacian linear systems in order to improve the convergence of iterative linear solvers. This problem has been studied in the literature from different perspectives in the classical case of the "combinatorial" Laplacian (see, e.g., D. A. Spielman & N. Srivastava, 2011). We are interested here in complex Laplacian matrices generalizing the classical case.
More specifically, we consider a U(1)-connection graph, that is, a graph where each oriented edge is endowed with a unit modulus complex number which is simply conjugated under orientation flip. A natural replacement for the usual graph Laplacian is then the so-called magnetic Laplacian, a Hermitian matrix which includes information about the graph's connection. Connection graphs and magnetic Laplacians appear, e.g., in the problem of angular synchronization (signal processing).
In the context of large and dense graphs, we study spectral sparsifiers of the magnetic Laplacian, i.e., spectral approximations based on subgraphs with few edges. Our approach relies on sampling variants of spanning forests using a custom determinantal point process, a distribution over edges that favours diversity (and which originates from quantum physics). In a word, the connected components of our spanning forests are either trees or cycle-rooted trees. The latter partially capture the angular inconsistencies of the connection graph, and thus provide a way to compress information contained in the connection. One of our contributions is to provide statistical guarantees for a choice of natural estimators of the connection Laplacian based on batches of spanning forests.
Interestingly, when the connection graph has weakly inconsistent cycles, samples of this distribution can be obtained by using a loop-erased random walk. This sampling algorithm is called CyclePopping and is actually rather performant in practice. The law of the number of steps to complete CyclePopping is also known exactly if the connection graph has weakly inconsistent cycles. We shall briefly discuss our contribution in the analysis of this algorithm.
Nicholas Landry, Realistically modeling diseases: from data to models and back again
Abstract: I discuss my process of attempting to accurately model the spread of diseases and the roadblocks and opportunities that emerged. I explain the process of developing an expert-informed contagion model through the lens of hospital-acquired C. difficile, where transmission is assumed to be mediated through infected surfaces, represented as a bipartite person-to-environment contact network. Secondly, I talk about a project that emerged from this study which examines the effectiveness of inferring a contact network from time-series data derived from both simple and complex contagion processes. I demonstrate that complex contagion processes learn dense network structure more effectively and learn more consistently over a wider range of parameters, whereas simple contagion can learn better, but for much narrower dynamical and network parameter regimes.
Jonas Juul, What does who-infected-who tell us about contagion?
Abstract: Many important challenges of our time are related to harmful contagion in networks. To mitigate such harmful contagion – be it misinformation, an epidemic, or something else – it is important to understand how the contagion spreads, and what its impact could be. In recent years, studying the structure of cascades – rooted, directed, acyclic graphs indicating who infected whom in the network – has provided a new way of getting insights about the spreading mechanism and contagion impact. In this talk, I will demonstrate how cascade structure can reveal the impact of future mutant strains in epidemics, whether super spreaders drive online diffusion, and whether false and true news diffuses similarly online or not. I will end the talk with a brief discussion of our future work: studying COVID-19 diffusion cascades in Denmark, and what we hope to learn from this. Relevant work:
Vosoughi et al., Science, 2018
Goel et al., Management Science, 2016
Juul & Strogatz, Physical Review Research, 2020
Juul & Ugander, Proceedings of the National Academy of Sciences, 2021.
Contributed talks
Matteo Sfragara, Competing first-passage percolation on the configuration model
Abstract: In this talk we will discuss competing first passage percolation on graphs generated by the configuration model, where two infection types compete to invade the vertices in the graph. Initially, two uniformly chosen vertices are infected with type 1 and type 2 infection, respectively, and the infection then spreads via nearest neighbors. The time it takes for the type 1 (resp. 2) infection to traverse an edge e is given by a random variable X_1(e) (resp. X_2(e)) and, if the vertex at the other end of the edge is still uninfected, it then becomes type 1 (resp. 2) infected and immune to the other type.
Matthew de Courcy-Ireland, Spectral Geometry of Graphs in Applications
Abstract: We introduce metric graph models able to describe transport in complicated networks. In particular we look at explicit examples of isospectral but not isoscattering graphs and explain the mechanism how this happens. Two analytic approaches are presented:
— via the graphs' M-functions (response operators, Dirichlet-to-Neumann maps)
— by inspecting values of the eigenfunctions at the contact points.
Our studies are motivated by recent experiments with microwave cavities.
Yu Xing, Detecting Communities from Equilibria of Nonlinear Opinion Dynamics
Abstract: In this presentation we will study community detection for a nonlinear opinion dynamics model from its equilibria. It is assumed that the underlying network is generated from a stochastic block model with two communities, where agents are assigned with community labels and edges are added independently based on these labels. Agents then update their opinions following a nonlinear rule that incorporates saturation effects on interactions. In the case with a single equilibrium available, we propose a community detection algorithm based on k-means. It is shown that the algorithm can detect most community labels (that is, achieving almost exact recovery), if the two communities differ in size and link probabilities. When the two communities are identical in size and link probabilities, and the inter-community connections are denser than intra-community ones, the algorithm can achieve almost exact recovery under negative influence weights but fails under positive influence weights. Utilizing the fixed point equation and spectral methods, we also propose a detection algorithm based on multiple equilibria, which can detect the communities in the case with positive influence weights. Numerical experiments demonstrate the effectiveness of the proposed algorithms.
Dhrubajyoti Biswas, Adaptive and symmetry breaking higher-order interactions in coupled phase oscillators
Abstract: One of the celebrated models used to study the ubiquitous phenomena of synchronization is the Kuramoto model of phase oscillators. This model has been studied in great detail in literature [1, 2] and has been extended to different coupling scenarios including multilayered, adaptive, and higher-order interactions. In this talk, I will focus on recent results on generalized multi-layered adaptive systems [3] and symmetry-breaking higher-order interactions [4] in the context of coupled Kuramoto phase oscillator models.
[1] Juan A Acebrón, Luis L Bonilla, Conrad J Pérez Vicente, Félix Ritort, and Renato Spigler. The kuramoto model: A simple paradigm for synchronization phenomena. Reviews of modern physics, 77(1):137, 2005.
[2] Shamik Gupta, Alessandro Campa, Stefano Ruffo, et al. Statistical physics of synchronization, volume 48. Springer, 2018.
[3] Dhrubajyoti Biswas and Sayan Gupta. Effect of adaptation functions and multilayer topology on synchronization. Phys. Rev. E, 109:024221, Feb 2024.
[4] Dhrubajyoti Biswas and Sayan Gupta. Symmetry-breaking higher-order interactions in coupled phase oscillators. Chaos, Solitons & Fractals, 181:114721, 2024
Pascal Helson, Graph signal processing to get insights into Parkinson’s disease
Abstract: When referring to graphs in brain imaging network analysis, the latter are derived from one of two main types of connectivities. One is called structural connectivity (SC) and based on anatomical structure obtained from diffusion MRI. The other one, functional connectivity (FC), is computed from the time series measured by M/EEG or fMRI. FCs are thus not directly reflecting the anatomy but more the activity of the brain. Classical graph theory measures have been applied to such brain networks but they lack of clear interpretability. One big question remaining concerns the link between these temporal signals and the structure on which they lie. Recently a method - called graph signal processing (GSP) - has been developed to tackle this question, hence offering new avenues on our understanding of their relationship. In particular, it gives new insights on the coupling between anatomy and function. This method is still very new and has been mainly applied on DTI (SC) + fMRI data on healthy subjects. Here we use GSP to analyse MEG data and compare the results obtained between two groups, healthy controls and Parkinson’s disease (PD) patients. We found changes in the visual and visual-motor cortex confirming and completing previous results on the accelerating ageing effect of PD.
Vincent Grande, Relating local features and global topology of networks and point clouds: Learning from the harmonic spaces of Hodge-Laplacians
Abstract: Extracting higher-order information that (a) is localised on the point/node level while at the same time (b) reflecting the global topological and structural features from a network or point cloud is not an easy task. We present Topological Point Cloud Clustering (TPCC), a new method to cluster nodes or points in an arbitrary network or point cloud based on their contribution to global topological features. TPCC considers the harmonic spaces of a family of associated Hodge Laplacians, higher-order generalisations of the Graph Laplacian, to synthesize desirable features. Pooling these features back to the node level and using a classical clustering approach, we can segment proteins into topologically different parts, detect anomalous points in manifolds or study different regimes in the state spaces of dynamical systems. By focusing not just on a single matrix but on a whole set of Hodge-Laplacians associated to an appropriately constructed simplicial complex, we can leverage a far richer set of topological features to characterize the data points and benefit from the relative robustness of topological techniques against noise.
Based on: Vincent P. Grande and Michael T. Schaub: "Topological Point Cloud Clustering", Proceedings of the 40th International Conference on Machine Learning (ICML 2023). https://arxiv.org/abs/2303.16716
Arvind Kumar, Network structure and activity dynamics relationship in neural networks in the brain
Abstract: I will briefly review some key aspects of the connectivity of different brain regions and describe how they may contribute to the network activity. The main focus will be on some features of neuron morphology that give rise to structural inhomogeneities in terms of in- and out-degrees of the neurons. I will show small deviations from an isotropic network can lead to qualitatively different dynamical properties.
Marco Nurisso, Interactions and peculiarities of simplicial dynamical models
Abstract: Simplicial dynamical systems have emerged as a diverse and intriguing class of models that can capture the dynamics of interacting agents placed on the simplices of a simplicial complex. Being elegantly formalized with the tools of discrete differential geometry, these models reveal interesting relationships between topology, geometry and the system’s dynamical behavior. Starting from the simplicial model of synchronization of Millán et al. (2020), we scrutinize their mathematical formulation to give a microscopic interpretation of their interactions. These include both effective higher-order and self-interactions when the complex is locally non-manifold-like. This naturally leads us to establish an equivalence between the simplicial model and its pairwise counterpart under the condition of the simplicial complex being a manifold. Then, we will discuss how such peculiarities originate in the structure of the combinatorial Hodge Laplacian, which encodes a diffusion process between simplices that cannot be thought of as diffusion in the “standard” sense.
Minh Tuan Pham, Triads Formation in Signed Social Networks: Theories and Experiments
Abstract: Despite a large number of works studying the organising principles of signed social networks, most have been formulated without being confronted with longitudinal data. One of the most common modelling assumptions is that individuals in a triad tend to simultaneously adjust both their direct social relationships and indirect ones (with contacts of their contacts). We show how models based on this assumption fail in explaining different temporal patterns observed in real-world societies, while a minimal model, which does not rely on this assumption, can accurately reproduce these patterns.
Xin Shen, Clustering social networks with uncertain edges following the possible worlds semantics
Abstract: The data produced in social network research are often rich: examples include the wealth of information found on social media, questionnaires inspecting different types of social ties and actor attributes, and archival records. Yet at the same time, these data may contain measurement errors or biases. For example, when researchers use questionnaires to construct relationship networks, people may remember incorrectly and give inaccurate answers. In general, the existence of edges in a social network may be uncertain, because of the inherent uncertainty in data collection processes. To capture this uncertainty, it has been suggested to assign probabilities to each pair of nodes, representing the likelihood of an edge existing between them. Instead of simplifying networks into strictly yes-or-no connections, preserving uncertainty through probabilities can offer richer insights.
Registration / Application
The joint application form for all four program workshops is found in the menu on the left under "Application" or at this link.
If you would like to participate, please register at this link by Wed, 21 February 2024 (anywhere on Earth). In particular if you require accommodation, travel or visa support, it is critical that you apply by this deadline.
After this deadline review of applications will begin and results communicated within three weeks. Later applications are considered on a rolling basis, subject to remaining capacity.
CAUTION! Occasionally scammers contact participants claiming to assist you with accommodation and travel arrangements etc.
Please be vigilant and do not share information with them! Also, please notify the organizers if you are in any doubt about the legitimacy of an approach, and never hesitate to contact us with any further questions.